Página inicial > 7º ano/conteúdo > NÚMEROS INTEIROS

NÚMEROS INTEIROS

No conjunto dos números naturais operações do tipo

9 - 5 = 4 é possível

5 – 5 = 0 é possível

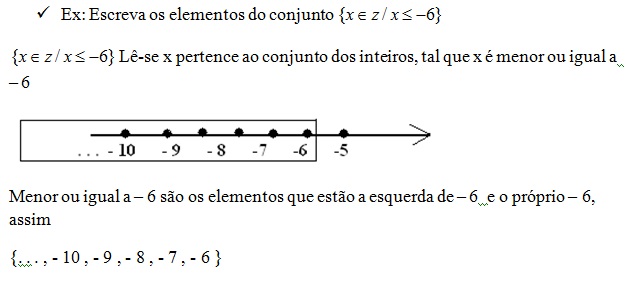
5 – 7 = ? não é possível e para tornar isso possível foi criado o conjunto dos números inteiros representados por Z.

Z = { . . . , - 4 , - 3 , - 2 , - 1 , 0 , 1 , 2 , 3 , 4 , . . . }

Imagine uma equipe de futebol que faz 5 gols e leva 3 ela ganha o jogo com saldo positivo de 2 gols indicamos por +2 .

Imagine agora que este mesma equipe de futebol faz 3 gols e leva 3 gols, neste caso o jogo é empate e o saldo de gols é zero, ou seja, nulo.

Agora se esta equipe de futebol faz 2 gols e leva 5 gols ela perde o jogo com saldo negativo de 3gols representado por – 3 ,é o mesmo que 2 – 5 = - 3 .

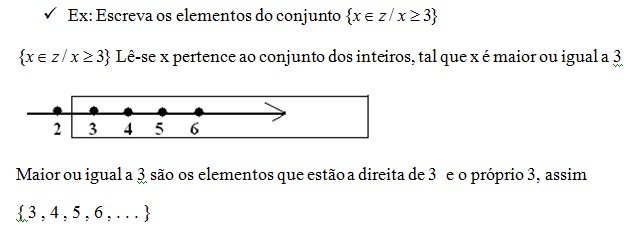
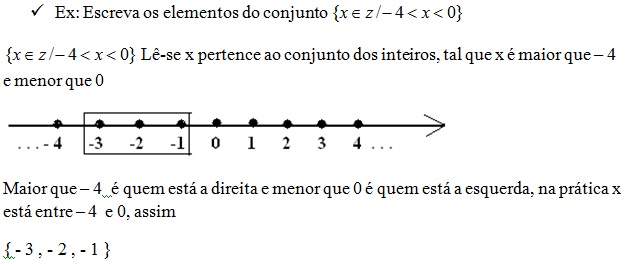
O conjunto dos números inteiros é composto por três tipos de números:

Positivos ( 1, 2 , 3 , 4 , ...)

Nulo ( 0 )

Negativos ( . . . , - 4 , - 3 , - 2 , - 1 )

Subconjuntos dos inteiros ( Z )

Observe o conjunto Z = { . . . , - 4 , - 3 , - 2 , - 1 , 0 , 1 , 2 , 3 , 4 , . . . }

Subconjuntos são conjuntos com elementos que pertencem a Z.

Para dar nome aos subconjuntos vamos sempre nos referir apenas a um dos nomes, positivo, negativo ou nulo.

Z* o asterisco indica a ausência do zero, logo nesse conjunto vai ter dois tipos de números, positivos e negativos se tem dois tipos de números vamos dar nome usando o que não tem que é o nulo, assim.

Z* é conjunto dos números inteiros não-nulos { . . . , - 3 , - 2 ,- 1 , 1 , 2 , 3 , . . . }

Z₊ significa que nesse conjunto terá o zero e os números positivos, veja tem dois tipos de números, então o nome é dado pelo que não tem que os negativos.Assim

Z₊ é conjunto dos números inteiros não-negativos { 0 , 1 , 2 , 3 ,. . . }

Z _-significa que nesse conjunto terá o zero e os números negativos, veja tem dois tipos de números, então o nome é dado pelo que não tem que os positivos.Assim

Z_- é conjunto dos números inteiros não-positivos { . . . , - 3 , - 2 , - 1 , 0 }

Z*₊ significa que não tem o zero e nem número negativo, portanto nesse conjunto só tem números positivos, só tem um tipo de número, nesse caso o conjunto recebe o nome com esse tipo de número.

Z*₊ é conjunto dos números inteiros positivos { 1 , 2 , 3 , . . . }

Z*_- significa que não tem o zero e nem número positivo, portanto nesse conjunto só tem números negativos, só tem um tipo de número, nesse caso o conjunto recebe o nome com esse tipo de número.

Z*_- é conjunto dos números inteiros negativos { -1 ,- 2 , -3 , . . . }

Reta numérica

Podemos representar os elementos do conjunto dos números inteiros na reta numérica, marcamos o ponto de origem que é o zero para a esquerda escrevemos os números negativos e para a direita os números positivos.

Observe na reta que 2 é maior que 1, o 4 é maior que 3, isso dar a você a noção de que o número maior é aquele que está a direita do outro, assim 0 é maior que -1 ,e – 3 é maior que – 4 , os números negativos crescem numericamente para a esquerda em termo de valor quanto mais ele cresce menos ele vale, assim – 35 é maior que – 58 .

Número oposto ou simétrico

São números que ficam a uma mesma distância do zero na reta numérica.

Ex: 1 e – 1 , 3 e – 3 , 7 e – 7 , 25 e – 25 na prática oposto é o mesmo número com sinal contrário.

Valor absoluto

Valor absoluto de um número é a idéia de quantidade que ele representa,ou seja, não consideramos o sinal de + ou de - .

Ex: +3 valor absoluto 3

- 5 valor absoluto 5

+ 14 valor absoluto 14

- 24 valor absoluto 24

Comparação entre números inteiros

A comparação de números inteiros e feita utilizando os símbolos ≤ ( menor ou igual ), ≥ ( maior ou igual ), < ( menor ) e > ( maior ). Não esqueça de que o número que está a direita do outro na reta é sempre maior.

Ex: 4 > 2 , - 2 > - 5 , 0 < 5

Veja outras aplicações dos sinais acima.

Adição e subtração

Para somar ou subtrair números inteiros é necessário aprender duas regrinhas que facilitarão em muito o calculo das operações.

1° Quando dois ou mais números inteiros tem o mesmo sinal somamos e conservamos o mesmo sinal.

Ex: + 2 + 3 = + 5

– 5 – 4 = - 9

+ 2 + 3 + 4 = + 9

– 2 – 3 – 1 – 2 – 4 = – 1 2

+ 2 + 8 + 1 + 4 + 2 = +17

OBS: o sinal de + nos resultados não é obrigatório. Poderia ser:

+ 2 + 3 = 5 + 2 + 3 + 4 = 9

2° Quando dois números inteiros têm sinais diferentes subtraímos ( maior – menor )valor absoluto e conservamos o sinal do número de maior valor absoluto.

Ex: + 2 – 3 subtraímos 3 – 2 que dar 1 e conservamos o sinal do número de maior valor absoluto que é 3, assim + 2 – 3 = – 1

Ex: - 5 + 3 subtraímos 5 – 3 que dar 2 e conservamos o sinal do número de maior valor absoluto que é 5, assim – 5 + 3 = – 2

Ex: + 8 – 3 subtraímos 8 – 3 que dar 5 e conservamos o sinal do número de maior valor absoluto que é 8, assim + 8 – 3 = 5 sinal de + no resultado não precisa colocar.

EXEMPLO: Calcule o valor de – 2 + 3 – 4 – 6 + 8 + 4

vamos resolver de dois em dois

– 2 + 3 – 4 – 6 + 8 + 4 sinal contrário, subtrair e conserva sinal do maior = +1

+1 – 4 – 6 + 8 + 4 sinal contrário, subtrair e conserva sinal do maior = - 3

– 3 – 6 + 8 + 4 mesmo sinal, soma e conserva o mesmo sinal = - 9

– 9 + 8 + 4 sinal contrário, subtrair e conserva sinal do maior = - 1

– 1 + 4 sinal contrário, subtrair e conserva sinal do maior

3 o sinal de + não precisa colocar

OBS: fazer de dois em dois fica muito extenso, podemos fazer de uma forma mais prática, veja abaixo o mesmo calculo feito de maneira mais prática.

EXEMPLO: Calcule o valor de – 2 + 3 – 4 – 6 + 8 + 4

Pelo método prático vamos somar e conservar o sinal de todos os números positivo e somar e conservar o sinal de todos os números negativos.

– 2 + 3 – 4 – 6 + 8 + 4 positivos +3+8+4 = +15 e negativos – 2 – 4 – 6 = – 12

– 12 + 15 sinal contrário subtrai e conserva sinal do maior valor absoluto

+ 3

EXEMPLO: Calcule o valor de – 6 + 4 – 5 – 6 + 2 + 1 – 4 + 3

– 6 + 4 – 5 – 6 + 2 + 1 – 4 + 3 positivos +4+2+1+3 = +10 e negativos –6 –5 –6 –4 = –21

+ 10 – 21 sinal contrário subtrai e conserva o sinal do maior valor absoluto

– 11

OBS: quando a expressão começar com número positivo não é necessário colocar o sinal de + , Ex: + 10 – 21 basta escrever 10 – 21

Adição e subtração que envolvem ( ), [ ] e { }

Para resolver operações que envolvem parênteses, colchetes e chaves, devemos eliminar pela ordem ( ), [ ] e depois { }que vão está precedido de sinal mais ( + ) ou de menos ( - ) se for:

Precedido de sinal mais ( + ) eliminamos o parêntese e o sinal que o precede conservando todos que estão dentro dos parentes com seus sinais.

Ex: + (– 2 + 3 – 4 + 5 ) elimina ( ) e o + que está antes, só escrevemos o que está no ( )

– 2 + 3 – 4 + 5

Ex: + ( 5 – 3 – 5 + 6 )elimina ( ) e o + que está antes, só escrevemos o que está no ( )

5 – 3 – 5 + 6 o sinal de + do 5 só não aparece porque ele está no inicio

Ex: + (– 2 + 3 ) + ( 6 +4 ) o 6 não aparece sinal de + ,quando sair do ( ) ai tem que aparecer já que antes dele vai ter o 3 .

– 2 + 3 + 6 + 4

Precedido de sinal menos (– ) eliminamos o parêntese e o sinal que o precede trocando o sinal de todos que estão dentro dos parentes.

Ex: – (– 6 + 3 – 4 + 2 ) elimina ( ) e o – que está antes, e trocamos o sinal de cada número dentro do parêntese.

+6 – 3 + 4 – 2

Ex: – ( 5 + 1 – 5 + 2 ) elimina ( ) e o – que está antes, e trocamos o sinal de cada número dentro do parêntese.

– 5 – 1 + 5 – 2

Ex: – (– 3 + 5 ) – (– 8 + 4 ) elimina ( ) e o – que está antes, e trocamos o sinal de cada número dentro do parêntese.

3 – 5 + 8 – 4

EXEMPLO: Calcule o valor de – ( + 5 – 6 – 3 ) + (– 1 + 3 + 4 – 8 )

– ( + 5 – 6 – 3 ) + (– 1 + 3 + 4 – 8 ) os números que estão dentro do 1° parêntese trocam de sinal e os que estão dentro do 2° parêntese ficam com o mesmo sinal. O sinal de menos antes do 1° parêntese e o sinal de mais antes do 2° parêntese, serão eliminados.

– 5 + 6 + 3 – 1 + 3 + 4 – 8 soma positivos +6+3+3+4=+16 e negativos –5–1–8= –14

+16 – 14 subtrai e conserva o sinal do maior valor absoluto

+ 2

EXEMPLO: Calcule o valor de [– 2 + (– 5 + 4 –3 )] – ( + 4 – 2 + 1 )

[– 2 + (– 5 + 4 –3 )] – ( + 4 – 2 + 1 ) elimina os parêntese e os sinais que estão antes

[– 2 – 5 + 4 – 3 ] – 4 + 2 – 1 não tem sinal antes do colchete é porque é de +

– 2 – 5 + 4 – 3 – 4 + 2 – 1 soma os positivos +4+2=+6 e os negativos –2–5–3–4–1= –15

+6 – 15 subtrai e conserva o sinal do maior valor absoluto

– 9

EXEMPLO: Calcule o valor de 6+ { – 5 + 2 – [– 4 + 5 +2 + (– 1 + 2 – 4 )+ 2] – 1 }

6+ { – 5 + 2 – [– 4 + 5 +2 + (– 1 + 2 – 4 )+ 2] – 1 } eliminamos 1° o parêntese e o sinal de + , quem tá dentro fica do mesmo jeito.

6 + { – 5 + 2 – [– 4 + 5 + 2 – 1 + 2 – 4 + 2 ] – 1 } eliminamos 2° o colchete e o sinal de - , quem tá dentro troca de sinal.

6 + { – 5 + 2 + 4 – 5 – 2 + 1 – 2 + 4 – 2 – 1 } eliminamos 3° a chave e o sinal de + , quem tá dentro fica do mesmo jeito.

6 – 5 + 2 + 4 – 5 – 2 + 1 – 2 + 4 – 2 – 1 Somamos os positivos 6+2+4+1+4 = 17 e negativos – 5 – 5 – 2 – 2 – 2 – 1 = – 17

+17 – 17 sinal contrário, subtraímos 17 – 17 como é zero não tem sinal

EXEMPLO: Calcule o valor de { – 2 + 1 – [–3 + 5 + ( 3 – 4 ) + 1] – 3 }

{ – 2 + 1 – [–3 + 5 + ( 3 – 4 ) + 1] – 3 } eliminamos o parêntese

{ – 2 + 1 – [– 3 + 5 + 3 – 4 + 1 ] – 3 } eliminamos o colchete

{ – 2 + 1 + 3 – 5 – 3 + 4 – 1 – 3 } não tem sinal antes da chaves então é +

– 2 + 1 + 3 – 5 – 3 + 4 – 1 – 3 positivos 1 + 3 + 4 = +8 e negativos –2 –5 –3 –1–3 = –14

+ 8 – 14 sinal contrário subtrai e conserva sinal do maior valor absoluto

– 6

Multiplicação de números inteiros

Para multiplicar dois ou mais números inteiros, multiplicamos os algarismos e o sinal do resultado será:

Positivo se os dois fatores tiverem o mesmo sinal.

Ex: ( + 2 ) . ( + 3 ) = + 6 e (– 5 ) . (– 2 ) = + 10

Negativo se os dois fatores tiverem sinais diferentes.

Ex: ( + 3 ) . (– 4 ) = – 12 e (– 5 ) . ( + 4 ) = – 20

Pelo método prático, multiplicamos os algarismos e fazemos o que chamamos de jogo de sinal que vale para multiplicação e divisão.

( + ) por ( + ) = +

(– ) por (– ) = +

( + ) por (– ) = –

(– ) por ( + ) = –

É muito importante você dominar bem o jogo de sinal.

Ex: (– 2 ) . ( + 3 ) . (– 4 ) multiplicamos 2 vezes 3 e fazemos o jogo de sinal

(– 6 ) . (– 4 ) multiplicamos 6 vezes 4 e fazemos o jogo de sinal

+ 24

Ex: ( + 5 ) . (– 3 ) . (– 2 ) . ( + 4 ) multiplicamos 5 vezes 3 e fazemos o jogo de sinal

(– 15 ) . (– 2 ) . ( + 4 ) multiplicamos 15 vezes 2 e fazemos o jogo de sinal

( + 30 ) . ( + 4 ) multiplicamos 30 vezes 4 e fazemos o jogo de sinal

120 não precisa colocar sinal de +

Pelo método prático

Ex: (– 2 ) . ( + 3 ) . (– 4 ) multiplicamos 2 . 3 . 4 =24 e fazemos o jogo de sinal – por + que dar – fazemos esse – por + que dar - , assim,

(– 2 ) . ( + 3 ) . (– 4 ) = – 24

Ex: ( + 5 ) . (– 3 ) . (– 2 ) . ( + 4 ) multiplicamos 5 . 3 . 2 . 4 = 120 e fazemos o jogo de sinal em sequencia + por – = – por – = + por + = + , logo

( + 5 ) . (– 3 ) . (– 2 ) . ( + 4 ) = + 120

Divisão de números inteiros

Dividimos os algarismos e fazemos o jogo de sinal.

Ex: (– 8 ) : ( + 2 ) dividimos 8 por 2 e fazemos o jogo de sinal

- 4

Ex: (– 12 ) : (– 3 ) dividimos 12 por 3 e fazemos o jogo de sinal

+ 4

Ex: (– 20 ) : ( + 10 ) : (– 2 ) dividimos 20 por 10 e fazemos o jogo de sinal

(– 10 ) : (– 2 ) dividimos 10 por 2 e fazemos o jogo de sinal

+ 5

Podemos ter exemplos envolvendo multiplicação e divisão, neste caso resolveremos a operação que vier primeiro.

Ex: (– 2 ) . ( + 15 ) : ( + 5 ). (– 3 ) : ( +6 ) multiplica 2 vezes 15 e faz o jogo de sinal

(– 30 ) : ( + 5 ) . (– 3 ) : ( + 6 ) divide 30 por 5 e faz o jogo de sinal

(– 6 ) . (– 3 ) : ( + 6 ) multiplica 6 vezes 3 e faz o jogo de sinal

( + 18 ) : ( + 6 ) divide 18 por 6 e faz o jogo de sinal

+ 3

Potênciação em Z

Já vimos a potência nos números naturais, ela vai está presente em cada conjunto que agente estudar , a forma de resolução será sempre a mesma. O expoente indicará quantas vezes a base será multiplicada por ela mesma.

Ex: 3⁴ o expoente 4 indica que a base 3 será multiplicada por Lea mesma 4 vezes

3 . 3 . 3 . 3 = 81

Ex: (– 3 )² o expoente 2 indica que a base (–3) será multiplicada por Lea mesma 2 vezes

(– 2 ) . (– 2 ) multiplicamos e fazemos o jogo de sinal

Ex: (– 5 )³ o expoente 3 indica que a base (–5) será multiplicada por Lea mesma 3 vezes

(– 5 ) . (– 5 ) . (– 5 ) multiplicamos e fazemos o jogo de sinal

– 125

Importante:

Toda base elevada a zero é sempre 1. Ex: ( + 3 )⁰ = 1 e (– 3 )⁰ = 1

Toda base elevada a 1 é igual a ela mesma. Ex: ( + 2 )¹ = 2 e (– 4 )¹ = – 4

Para base 1 devemos ter um certo cuidado. Veja os exemplos:

Ex: ( + 1 )² = ( + 1 ) . ( + 1 ) = + 1

(– 1 )⁴ = (– 1 ) . (– 1 ) . (– 1 ) . (– 1 ) = + 1

Note que se o expoente É PAR o resultado será positivo

Ex: ( + 1 )⁵ = ( + 1 ) . ( + 1 ) . ( + 1 ) . ( + 1 ) . ( + 1 ) = + 1

(– 1 )⁵ = (– 1 ) . (– 1 ) . (– 1 ) . (– 1 ) . (– 1 ) = – 1

Note que se o expoente É IMPAR o resultado terá o mesmo sinal da base

Quando a base é 1 é necessário saber essa regrinha, pois o 1 multiplicado por ele mesmo é sempre 1.

Ex: ( + 1 )¹⁰⁰⁰ não vamos colocar a base +1 mil vezes, como 1 multiplicado por ele mesmo é sempre 1 e expoente par o resultado é positivo, então

( + 1 )¹⁰⁰⁰ = + 1

Ex: (– 1 )¹⁰²⁸ não vamos colocar a base – 1 mil e vinte e oito vezes, como 1 multiplicado por ele mesmo é sempre 1 e expoente par o resultado é positivo, então

(– 1 )¹⁰⁰⁰ = + 1

Ex: ( + 1 )²²³ não vamos colocar a base +1 duzentas e vinte e três vezes, como 1 multiplicado por ele mesmo é sempre 1 e expoente impar leva para o resultado o sinal da base, então

( + 1 )²²³ = + 1

Ex: (– 1 )²²³ não vamos colocar a base –1 duzentas e vinte e três vezes, como 1 multiplicado por ele mesmo é sempre 1 e expoente impar leva para o resultado o sinal da base, então

( + 1 )²²³ = – 1

Propriedades

As propriedades de potências são sempre válida para qualquer base.

Multiplicação de mesma base - Conservamos a base e somamos os expoentes.

Ex: (– 2 )³ . (– 2 )⁴ = (– 2 )^{3 + 4} = (– 2 )⁷

( + 3 )⁵ . ( + 3 )³ = ( + 3 )^{5 + 3} = ( + 3 )⁸

Divisão de mesma base – Conservamos a base e subtraímos os expoentes.

Ex: (– 7 )⁷ : (– 7 )⁴ = (– 7 )^{7 – 4} = (– 7 )³

( + 1 )⁵ : ( + 1 )² = ( + 1 )^{5 – 2} = ( + 1 )³

Potência de potência – Conservamos a base e multiplicamos os expoentes.

Ex: [ (– 3 )² ]⁶ = (– 3 )^{2 . 6} = (– 3 )¹²

Produto ou quociente - Conservamos cada base e multiplicamos os expoentes.

Ex: [ (– 2 )³ . ( + 3 )² ]⁵ conservamos a base – 2 e multiplicamos 3 . 5 ,mantemos o sinal que separa as duas bases, depois conservamos a base + 3 e multiplicamos 2 . 5 .

(– 2 )¹⁵ . ( + 3 )¹⁰

Ex: [ (– 5 )⁴ : ( + 2 )⁵ ]² conservamos a base – 5 e multiplicamos 4 . 2 ,mantemos o sinal que separa as duas bases, depois conservamos a base + 2 e multiplicamos 5 . 2 .

(– 5 )⁸ : ( + 2 )¹⁰

Expressões numéricas

Para se resolver uma expressão algébrica, devemos obedecer a uma sequencia de resolução.

1° as potências , 2° multiplicações e/ou divisão e 3° adição e subtração.

Obedecendo a ordem de parentes, colchetes e chaves.

Ex: Resolva a expressão [ (– 2 ) . (– 3 ) + 4 ] : ( + 5 ) – ( + 7 )

[ (– 2 ) . (– 3 ) + 4 ] : ( + 5 ) – ( + 7 ) dentro do colchete fazemos a multiplicação

[ + 6 + 4 ] : ( + 5 ) – ( + 7 ) resolve o colchete

10 : ( + 5 ) – ( + 7 ) resolve a divisão

+ 2 – ( + 7 ) eliminamos o parêntese

+2 – 7 sinal contrário subtrai e conserva o sinal do maior valor absoluto

– 5

EX: Resolva a expressão (– 4 ) + [ (– 8 ) : (– 2 ) . ( + 3 ) – 4 ] + (– 2 ) . (– 5 )

(– 4 ) + [ (– 8 ) : (– 2 ) . ( + 3 ) – 4 ] + (– 2 ) . (– 5 )

Dentro do colchete tem a divisão e a multiplicação faz a que está 1° e a multiplicação fora do colchete também pode ser feita.

(– 4 ) + [ ( + 4 ) . ( + 3 ) – 4 ] + ( + 10 )dentro do colchete faz a multiplicação

(– 4 ) + [ + 12 – 4 ] + ( + 10 ) podemos eliminar o colchete e o parêntese

– 4 + 12 – 4 + 10 soma os positivos + 12 + 10 = + 22 e negativos – 4 – 4 = – 8

+ 22 – 8 subtrai e conserva o sinal do maior valor absoluto

EX: Resolva a expressão (– 2 )³ + [ (– 1 )⁵ + (– 2 ) . ( + 5 ) ] – (– 3 )²

(– 2 )³ + [ (– 1 )⁵ + (– 2 ) . ( + 5 ) ] – (– 3 )² tendo potência, resolva 1° a potência

(– 8 ) + [ (– 1 ) + (– 2 ) . ( + 5 ) ] – ( + 9 ) resolve a multiplicação do colchete

(– 8 ) + [ (– 1 ) + (– 10 )] – ( + 9 ) podemos eliminar todos os parênteses

– 8 + [– 1 – 10 ] – 9 elimina o colchete

– 8 – 1 – 10 – 9 todos tem o mesmo sinal soma e conserva o mesmo sinal

– 28

Menu

Pesquisar no site

Contato

NÚMEROS INTEIROS